I have recently discussed the problem of changepoint detection from a frequentist point of view. In that framework, changepoints were inferred using a maximum likelihood estimation (MLE) approach. This gave us point estimates for the positions of the changepoints.

In this post I will present the solution to the same problem from a Bayesian perspective, using a mix of both theory and practice (using the $\small{\texttt{pymc3}}$ package). The frequentist and Bayesian approaches give actually very similar results, as the maximum a posteriori (MAP) value, which maximises the posterior distribution, coincides with the MLE for uniform priors. In general, despite the added complexity in the algorithm, the Bayesian results are rather intuitive to interpret.

Just as for the frequentist case, the Bayesian problem admits a solution that can be expressed in analytical form. In the first part of this blog post I will first present this solution, which is based on the excellent chapter 5 of the book “Numerical Bayesian Methods Applied to Signal Processing” by Joseph O. Ruanaidh and William Fitzgerald.

In the second part of this post I will present numerical solutions based on the $\small{\texttt{pymc3}}$ package, for different type of problems including multiple changepoints.

1. Single changepoint: analytic Bayesian solution

Let us assume that we only have one changepoint and that the distributions before and after it are well modeled by stationary Gaussian distributions $\mathcal{N}(\mu,\sigma)$ with mean $\mu$ and variance $\sigma^2$.

We then model each of $i=1,\dots,N$ observed data points $\textbf{d} = \{d_1,..,d_N\}$ in the following way,
$$d_i = \left\{ \begin{array} $\mathcal{N}(\mu_1,\sigma) \ \mathrm{for} \ t<\tau \ \ \ \ \ (i.) \\ \mathcal{N}(\mu_2,\sigma) \ \mathrm{for} \ t\geq\tau \ \ \ \ \ (ii.) \end{array} \right.$$
in which $\mu_1$ and $\mu_2$ are the mean values before and after the changepoint, respectively.

We now introduce the Bayesian point of view. First of all, note that the only known quantities in the expressions i. and ii. are the observed data $d_i$ and we want to infer the unknowns $\mu_1,\mu_2,\sigma,\tau$ based on the observed data.

“Inferring the model parameters by looking at the observed data” immediately rings like Bayes’ theorem. Let’s write this theorem in all its glorious form, specifying it for our problem,

and discuss separately each term in eq. (\ref{eq:Bayes}):

• $\mathbb{P}(\mu_1,\mu_2,\sigma,\tau|\textbf{d})$: posterior distribution. It is the quantity that we are interested in (“inferring the model parameters by looking at the observed data”).
• $\mathbb{P}(\textbf{d}|\mu_1,\mu_2,\sigma,\tau)$: likelihood function. It represents how likely it is to observe the data we have, for a given choice of the model parameters. Maximising the likelihood function is the basis for the maximum likelihood estimation (MLE) method that was used in the previous blog post.
• $\mathbb{P}(\mu_1,\mu_2,\sigma,\tau)$: prior distribution. It encodes our information on the model parameters, before observing the data.
• $\mathbb{P}(\textbf{d})$: evidence. It is a measure of how well our model fits the data (how good our model is). For our specific case it tells us whether or assumptions of assuming one changepoint and a Gaussian process is a good one. It is often difficult to evaluate this term analytically and for the purpose of this discussion, it can be disregarded as being just a multiplication factor.

In the absence of specific prior information on the data, we are going to use non-informative prior distributions, assuming that $\mu_1,\mu_2,\sigma$ and $\tau$ are all independent random variables,
$$\begin{eqnarray} \mathbb{P}(\mu_1) = k_1 & \\ \mathbb{P}(\mu_2) = k_2 & \\ \mathbb{P}(\log\sigma) = k_3 & \Rightarrow \mathbb{P}(\sigma)=\frac{1}{\sigma} \\ \mathbb{P}(\tau) = k_4 \end{eqnarray}$$

where $k1, k_2, k_3$ and $k_4$ are all unspecified constants. Note how the resulting priors are all _improper priors, in the sense that they are not integrable (and in particular, they don’t integrate to 1). Note also who the prior for the variance is not uniform but goes like $1/\sigma$, consistent with Jeffrey’s principle for non-informative priors.

Finally… here comes the fun part! The objective of our analytic treatment is to find the posterior distribution of the changepoint $\tau$, or $\mathbb{P}(\tau|\textbf{d})$. This is obtained by marginalizing the posterior distribution $\mathbb{P}(\mu_1,\mu_2,\sigma,\tau|\textbf{d})$ with respect to the nuisance (i.e., “uninteresting”) parameters $\mu_1,\mu_2,\sigma$. In other words, we are not interested in the whole multi-dimensional posterior distribution, which will be impossible even to plot. Instead, we decide to have a lower-dimensional representation of the posterior distribution by looking only at one particular dimension ($\tau$) and integrating over the other dimensions.

Marginilizing with respect to $\mu_1,\mu_2,\sigma$ means nothing more than summing (for discrete distributions) or integrating (for continuous distributions) with respect to the nuisance parameters, like so:

in which we have used Bayes’ theorem and the definitions of the priors that we introduced above.

Here the process that is needed to obtain $\mathbb{P}(\tau|\textbf{d})$:

• calculate likelihood function $\mathbb{P}(\textbf{d}|\mu_1,\mu_2,\sigma,\tau)$
• integrate with respect to $\mu_1$
• integrate with respect to $\mu_2$
• integrate with respect to $\sigma$

Regarding integration with respect to $\mu_1$ and $\mu_2$, the following identity is useful:
$$\begin{equation} \int_{-\infty}^{\infty}\exp(-ax^2-bx-c)\,\textrm{d}x = \sqrt{\frac{\pi}{a}}\exp\left(\frac{b^2}{4a}-c\right)\ . \label{eq:intIdentity1} \end{equation}$$
Regarding integration with respect to $\sigma$, this other identity is useful:
$$\begin{equation} \int_0^{\infty}x^{\alpha-1}\exp(-Qx)\,\textrm{d}x=\frac{\Gamma(\alpha)}{Q^\alpha}\ , \label{eq:intIdentity2} \end{equation}$$
in which $\Gamma(\alpha)=\int_0^{\infty}x^{\alpha-1}\exp(-x)\,\textrm{d}x$ is the Gamma function.

1.1 Calculate likelihood function

This is based on our model definition, in which we are assuming that all of our data points from $1$ to $\tau$ can be modeled by a normal distribution $\mathcal{N}(\mu_1,\sigma)$ and the remaining ones by another normal distribution $\mathcal{N}(\mu_2,\sigma)$,
$$\begin{align} \mathbb{P}(\textbf{d}|\mu_1,\mu_2,\sigma,\tau) & =\prod_{i=1}^\tau \mathbb{P}(d_i|\mu_1,\sigma)\prod_{j=\tau+1}^N \mathbb{P}(d_j|\mu_2,\sigma) \propto \nonumber \\ & (2\pi\sigma^2)^{-N/2}\exp{\left\{-\frac{1}{2\sigma^2}\left[\sum_{i=1}^\tau (x_i^2+\mu_1^2-2\mu_1x_i) + \sum_{j=\tau+1}^N(x_j^2+\mu_2^2-2\mu_2x_j)\right]\right\}} \label{eq:likelihood} \end{align}$$

1.2 Integral with respect to $\mu_1$

We can use the identity eq. (\ref{eq:intIdentity1}) for this one, obtaining
$$\begin{align} \mathbb{P}(\mu_2,\sigma,\tau|\textbf{d}) & = \int_{-\infty}^{\infty} \mathbb{P}(\mu_1,\mu_2,\sigma,\tau|\textbf{d}) \,\textrm{d}\mu_1 \propto \nonumber \\ & \left(\frac{2\pi}{\tau}\right)^{1/2}(2\pi\sigma^2)^{-N/2} \exp{\left\{-\frac{1}{2\sigma^2}\left[\sum_{i=1}^\tau x_i^2-\frac{(\sum_{i=1}^\tau x_i)^2}{\tau} - \sum_{j=\tau+1}^N(x_j-\mu_2)^2\right]\right\}} \end{align}$$

1.3 Integral with respect to $\mu_2$

We use again the identity eq. (\ref{eq:intIdentity1}),
$$\begin{align} \mathbb{P}(\sigma,\tau|\textbf{d}) & = \int_{-\infty}^{\infty} \mathbb{P}(\mu_2,\sigma,\tau|\textbf{d}) \,\textrm{d}\mu_2 \propto \nonumber \\ & \frac{(2\pi\sigma^2)^{-(N-1)/2}}{(\tau(N-\tau)^{1/2})} \exp{\left\{-\frac{1}{2\sigma^2}\left[\sum_{i=1}^\tau x_i^2-\frac{(\sum_{i=1}^\tau x_i)^2}{\tau} - \frac{(\sum_{j=\tau+1}^N x_j)^2}{N-\tau}\right]\right\}} \end{align}$$

1.4 Integral with respect to $\sigma$

Using the expression in eq. (\ref{eq:intIdentity2}), this is the final result that we get:
$$\bbox[white,5px,border:2px solid red]{ \begin{align} \mathbb{P}(\tau|\textbf{d}) & = \int_{-\infty}^{\infty} \mathbb{P}(\sigma,\tau|\textbf{d}) \,\textrm{d}\sigma\propto \nonumber \\ & \frac{1}{\sqrt{\tau(N-\tau)}}\left[\sum_{k=1}^{N} x_k^2 - \frac{(\sum_{i=1}^{\tau}x_i)^2}{\tau} - \frac{(\sum_{j=\tau+1}^{N}x_j)^2}{N-\tau}\right]^{-(N-2)/2}\ \hspace{2cm} \label{eq:bayesian_final} \end{align} }$$

Now please stay focused as we are going to compare numerical results obtained with $\small{\texttt{pymc3}}$ against this very expression (\ref{eq:bayesian_final}) and we will find a very impressive matching!

2. Numerical Bayesian solution

In this section we are going to see how to use the $\small{\texttt{pymc3}}$ package to tackle our changepoint detection problem. I found $\small{\texttt{pymc3}}$ to be rather easy to use, particularly after a quick introduction to Theano. The key is understanding that Theano is a framework for symbolic math, it essentially allows you to write abstract mathematical expressions in python. Bonus point: it is possible to run Keras on top of Theano (not just on top of Tensorflow).

Before diving into the technical details of the implementation in $\small{\texttt{pymc3}}$, here are my observations regarding solving a changepoint detection problem using a naïve Markov Chain Monte Carlo approach:

• convergence can be made significantly faster using the right choice of priors (I know, it is sort of an obvious point…)
• because of my previous point, it is difficult to write an efficient algorithm without having some kind of manual inspection of the data. This means that it is difficult to think of a very general solution, one that does not require some tweaking of the parameters

And now… let’s start playing.

2.1 Multiple changepoint detection using pymc3 - in a nutshell

The main idea behind solving a multiple changepoint detection problem in $\small{\texttt{pymc3}}$ is the following: using multiple Theano switch functions to model multiple changepoints. This is quite a simple idea that shows the versatility of Theano.

Let’s make an example from scratch to show how the logic works. In this example we are going to:

• define two stochastic variables, $\mu$ and $\sigma$
• define the log-likelihood function
• initialize and then start the MCMC algorithm

Suppose we are expecting the data to contain two changepoints $\tau_1$ and $\tau_2$ such that we model the observed data points $d_i$ in the following way,

In this problem we have 6 unknown parameters: $\mu_1$, $\mu_2$, $\mu_3$, $\sigma$, $\tau_1$ and $\tau_2$. We want to use pymc3 to find posterior distributions for these parameters (so we are implicityly in a Bayesian framework).

Here is how we can do this in $\small{\texttt{pymc3}}$. First, we have to import the relevant packages (make sure you have installed $\small{\texttt{pymc3}}$ version 3.2 and $\small{\texttt{theano}}$),

1
2
3
4
5
6
7
8

import numpy as np
import scipy.stats as stats
from scipy.stats import norm
import pymc3 as pm
import theano
from theano import tensor as T
from pymc3.math import switch
import matplotlib.pyplot as plt

At this point we define some synthetic data that we are going to use as our testbed,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

np.random.seed(100) #initialize random seed
size1 = 1000 #size of first part (number of points)
size2 = 1000 #size of second part (number of points)
size3 = 1000 #size of third part (number of points)
N = size1+size2+size3 #total number of points
scale = 30 #standard deviation of distribution function across all three parts
loc1 = 1000 #mean of normal for first part
loc2 = 1100 #mean of normal for second part
loc3 = 800 #mean of normal for third part
d1 = norm.rvs(loc=loc1,size=size1,scale=scale) #randomly generates points for first part
d2 = norm.rvs(loc=loc2,size=size2,scale=scale) #randomly generates points for second part
d3 = norm.rvs(loc=loc3,size=size3,scale=scale) #randomly generates points for third part
data = np.hstack([d1,d2,d3]) #these are our final observation points
plt.plot(data) #let's have a look at our data
plt.show()

The code above defines two changepoints at positions 1000 and 2000, in which the mean value changes from 1000 to 1100 and then from 1100 to 800. The standard deviation is set at the value 30 for the whole dataset.

We want $\small{\texttt{pymc3}}$ to find all these parameters. Here is how we can do it:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

niter = 2000 #number of iterations for the MCMC algorithm
t = np.arange(0,N) #array of observation positions ('time')

with pm.Model() as model: # context management

    #define uniform priors
    mu1 = pm.Uniform("mu1",800,1100)
    mu2 = pm.Uniform("mu2",900,1200)
    mu3 = pm.Uniform("mu3",600,1000)
    sigma = pm.Uniform("sigma",1.e-3,100)
    tau1 = pm.DiscreteUniform("tau1",t.min(),t.max())
    tau2 = pm.DiscreteUniform("tau2",tau1,t.max())

    #define stochastic variable mu
    _mu = T.switch(tau1>=t,mu1,mu2)
    mu = T.switch(tau2>=t,_mu,mu3)

    #define formula for log-likelihood
    logp = - T.log(sigma * T.sqrt(2.0 * np.pi)) \
           - T.sqr(data - mu) / (2.0 * sigma * sigma)
    def logp_func(data):
        return logp.sum()

    #find out log-likelihood of observed data
    L_obs = pm.DensityDist('L_obs', logp_func, observed=data)

    #start MCMC algorithm
    start = pm.find_MAP()
    step = pm.NUTS(state=start)
    #iterate MCMC
    trace = pm.sample(niter, step, start=start, random_seed=123, progressbar=True)

In the code above, the interesting parts are the definitions of the stochastic variables $\mu$ and $\sigma$ and the definition of the log-likelihood function which is the same as in eq. (\ref{eq:likelihood}), after applying the logarithmic function,

Note that the changepoint variables $\small{\texttt{tau1}}$ and $\small{\texttt{tau2}}$ are initialized as uniform random variables. However, while $\small{\texttt{tau1}}$ spans the whole time domain from 1 to N (where N is the total number of data points), $\small{\texttt{tau2}}$ only spans the values from $\small{\texttt{tau1}}$ to N. In this way we ensure that $\small{\texttt{tau2}}$ > $\small{\texttt{tau1}}$.

The other trick is what we were discussing at the beginning of this section: the stochastic variable $\small{\texttt{mu}}$ is defined after first defining a dummy stochastic variable _$\small{\texttt{mu}}$. In essence, line 16 says that for all the values $\small{\texttt{t}}$ for which $\small{\texttt{tau2}}$>t (i.e., for all the values to the left of $\small{\texttt{tau2}}$), $\small{\texttt{mu}}$ takes the value _$\small{\texttt{mu}}$. Otherwise, it takes the value $\small{\texttt{mu3}}$. In this way, by using twice the switch function we achieve the objective of having a stochastic variables that changes according to whether $t<\tau_1$, $\tau_1\leq t < \tau_2$ or $t \geq \tau_2$.

Finally we can have a look at the result by plotting the trace:

1

pm.traceplot(trace[500:])

(You will see more about the $\small{\texttt{traceplot}}$ function in the next sections. And if you want to see how the plots for this example look like, you can skip immediately to Section 2.4.)

In the last part of this blog post I am going to list a series of problems that are solved using the code $
\small{\texttt{changepoint_bayesian.py}}$, which is written in python 3.5 and can be downloaded below,

This code is more general (but also more obscure) than the example given above. Using $\small{\texttt{changepoint_bayesian.py}}$ I will present the solution to a series of problems that range from the single-change-point detection case that was discussed in the analytic solution above (Section 1), up to a three-change-points case. The code can easily be generalized to more change points, it is in fact pretty much ready for it.

2.2 Single changepoint in the mean and comparison with theory

In this problem there is a changepoint at the position $\tau=2500$, where the mean value changes from $\mu_1=1000$ to $\mu_2=1020$, the standard deviation being the same at $\sigma=50$,
$$d_i = \left\{ \begin{array} $\mathcal{N}(1000,50) \ \ \mathrm{for} \ \ t<2500 \\ \mathcal{N}(1020,50)\ \ \mathrm{for} \ \ t \geq 2500 \end{array} \right.$$

To load this problem and see how the data look like, after downloading $\small{\texttt{changepoint_bayesian.py}}$ you can run the following lines in IPython:

1
2
3

In [1]: run changepoint_bayesian.py
In [2]: d = cpt_bayesian("1-cpt-mean")
In [3]: d.plot_data()

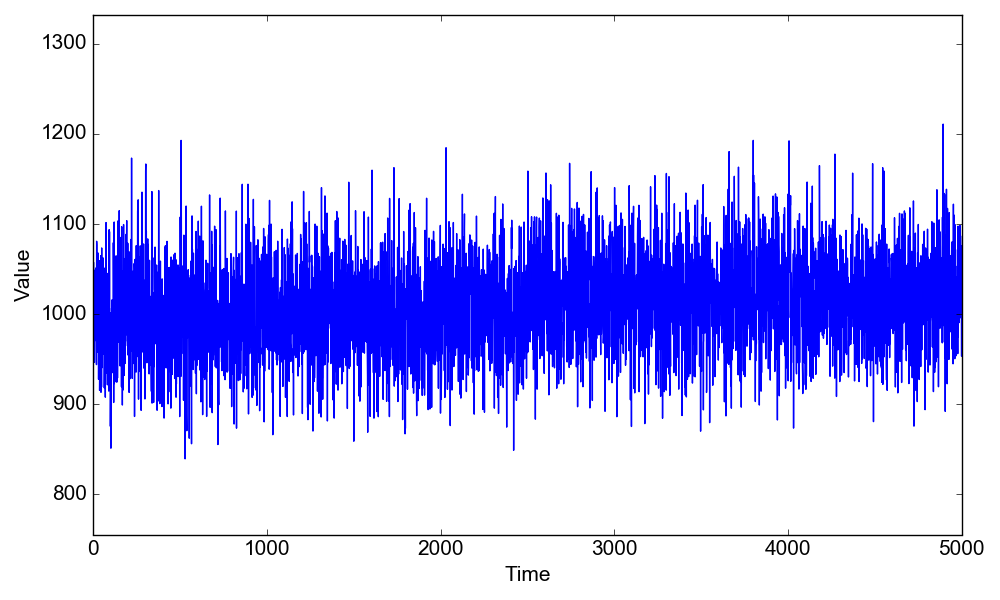
To find the posterior estimates for $\tau$, $\mu_1$, $\mu_2$ and $\sigma$ here is how we can proceed,

1
2
3
4
5
6
7

In [4]: d.find_changepoint()
Assigned NUTS to mu1_interval_
Assigned NUTS to mu2_interval_
Assigned Metropolis to tau1
Assigned NUTS to sigma_interval_
100%|████████████████████████████████████████████████████████████████████████████████████████████████████| 5000/5000 [00:27<00:00, 178.99it/s]
In [5]: d.plot_results()

and the corresponding trace plot is shown below,

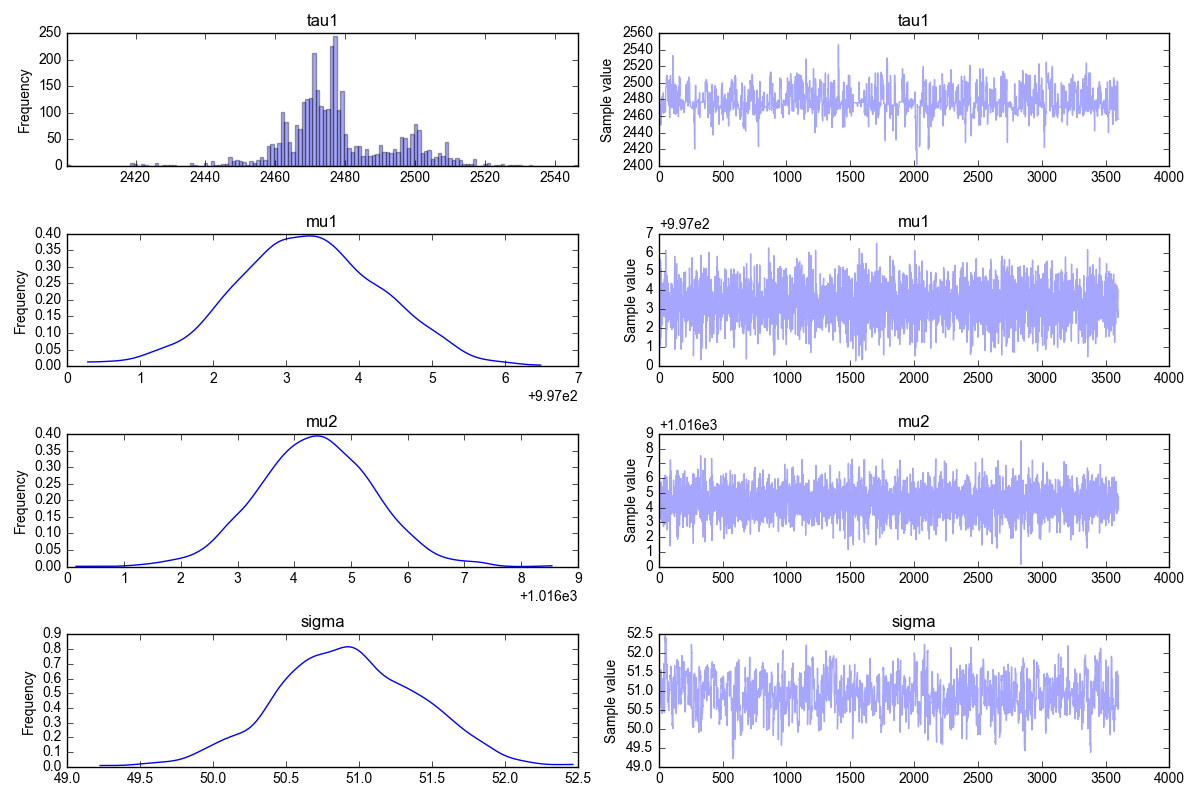
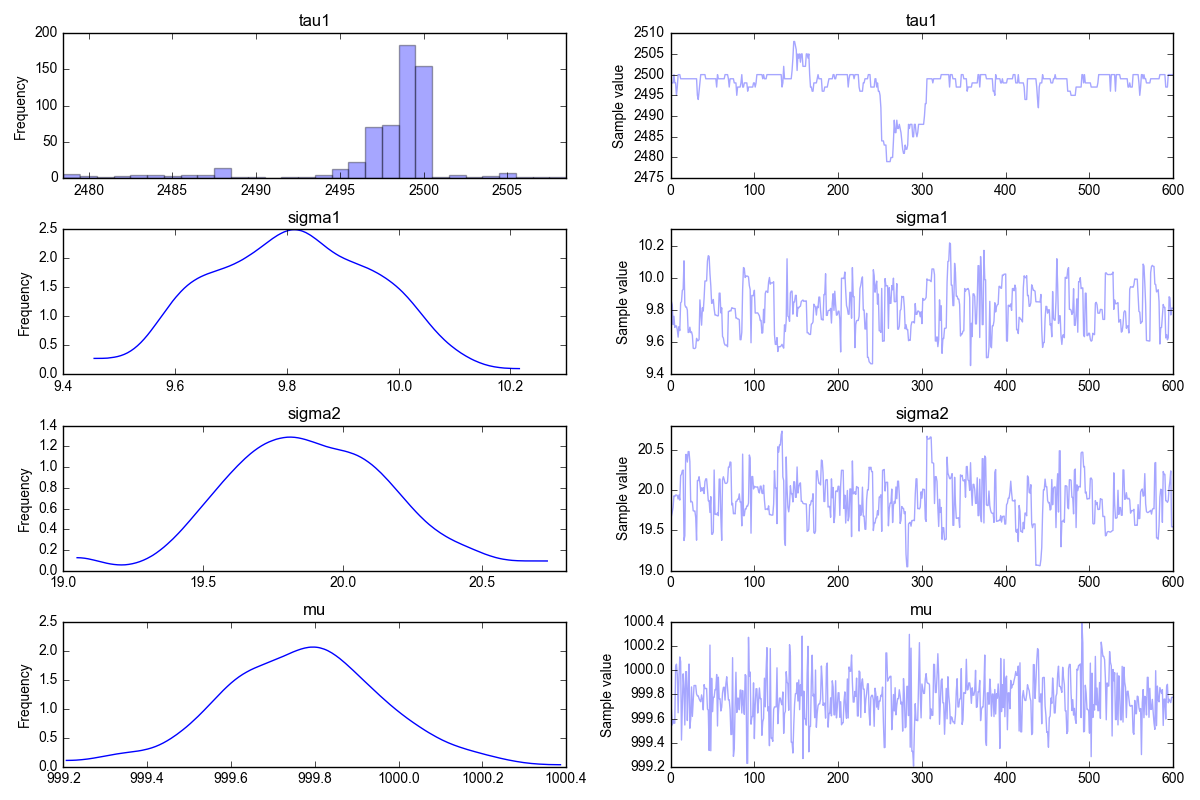
What is the trace plot telling us? We should first look at the right column. These are the results of the MCMC iterations. The first iterations have been filtered out, that’s where you would see that the algorithm has not yet converged. Instead, in all the plots on the right column you can see that the MCMC solution does not change much, i.e. we can confidently say that the algorithm has converged to its stationary solution (the posterior distribution). This means that the algorithm is now randomly sampling from the posterior distribution.

Now, what about the left column? These are simply the histograms of the data in the right column. If, as discussed, we believe the data on the right are all representative of the posterior distribution (i.e., the MCMC algorithm has converged) then these histograms are the answers to our problems: the marginals of the posterior distribution.

With reference to the figure above, here is how we interpret the data:

• the top left plot is the marginal $\mathbb{P}(\tau|\textbf{d})$
• the plot just below is the marginal $\mathbb{P}(\mu_1|\textbf{d})$
• the plot just below is the marginal $\mathbb{P}(\mu_2|\textbf{d})$
• the bottom left plot is the marginal $\mathbb{P}(\sigma|\textbf{d})$

When I first saw the top left plot, I was a bit skeptic about the result. This is not at all a smooth solution, I was expecting to see something “nicer”. And this is exactly why it is important to have analytical solutions to compare against!

Once we do that, once we compare the result for $\mathbb{P}(\tau|\textbf{d})$ as given by $\small{\texttt{pymc3}}$ against the analytical result given in eq. (\ref{eq:bayesian_final}), this is what we get

1

In [6]: d.plot_theory()

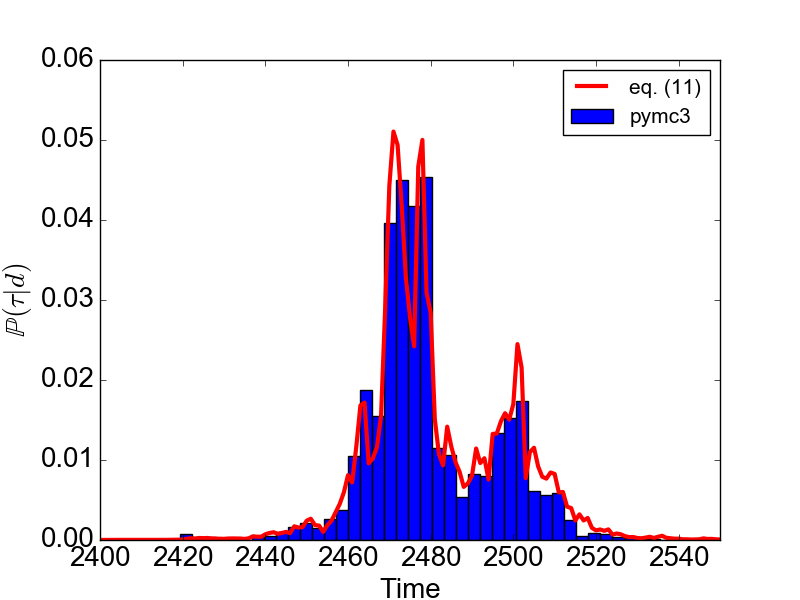
Wow, the simulation results are pretty close to the theory! And as you can see, the MCMC solution is able to reproduce non-trivial shapes of the probability distribution function. Way to go $\small{\texttt{pymc3}}$!

2.3 Single changepoint in the variance

In this problem, instead of the mean value we are going to change the variance from $\sigma_1=10$ to $\sigma_2=20$, keeping the same mean value $\mu=1000$, like so:
$$d_i = \left\{ \begin{array} $\mathcal{N}(1000,10) \ \ \mathrm{for} \ \ t<2500 \\ \mathcal{N}(1000,20)\ \ \mathrm{for} \ \ t \geq 2500 \end{array} \right.$$

Now, load the data and plot them. In IPython, run:

1
2
3

In [1]: run changepoint_bayesian.py
In [2]: d = cpt_bayesian("1-cpt-var")
In [3]: d.plot_data()

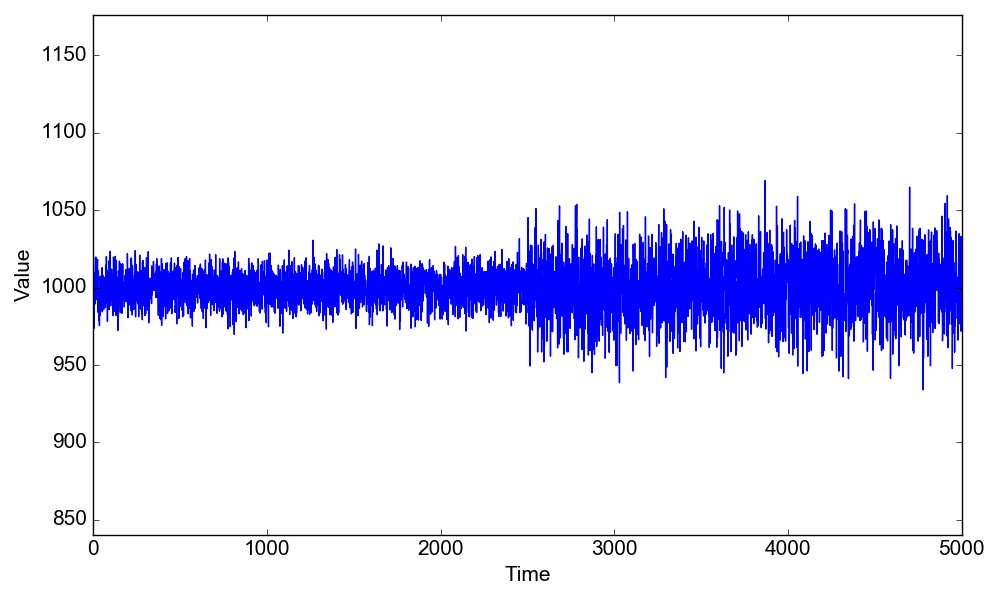
To find the posterior estimates for $\tau$, $\sigma_1$, $\sigma_2$ and $\mu$,

1
2
3
4
5
6
7

In [4]: d.find_changepoint()
Assigned NUTS to sigma1_interval_
Assigned NUTS to sigma2_interval_
Assigned Metropolis to tau1
Assigned NUTS to mu_interval_
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████| 2000/2000 [01:59<00:00, 22.59it/s]
In [5]: d.plot_results()

The resulting trace plot is given below. It shows that the posterior estimates are close to the true parameters.

2.4 Two changepoints in the mean

This is the same example given in Section 2.1. We are going to have two change points $\tau_1=1000$ and $\tau_2=2000$, with the mean value changing from $\mu_1=1000$ to $\mu_2=1100$ to $\mu_3=800$, keeping the same standard deviation $\sigma=30$ (this is the same example of section 2.1)
$$d_i = \left\{ \begin{array} $\mathcal{N}(1000,30) \ \ \mathrm{for} \ \ t<1000 \\ \mathcal{N}(1100,30)\ \ \mathrm{for} \ \ 1000 \leq t \geq 2000 \\ \mathcal{N}(800,30)\ \ \mathrm{for} \ \ t \geq 2000 \end{array} \right.$$

First, let’s load and plot the data. In IPython, run:

1
2
3

In [1]: run changepoint_bayesian.py
In [2]: d = cpt_bayesian("2-cpt-mean")
In [3]: d.plot_data()

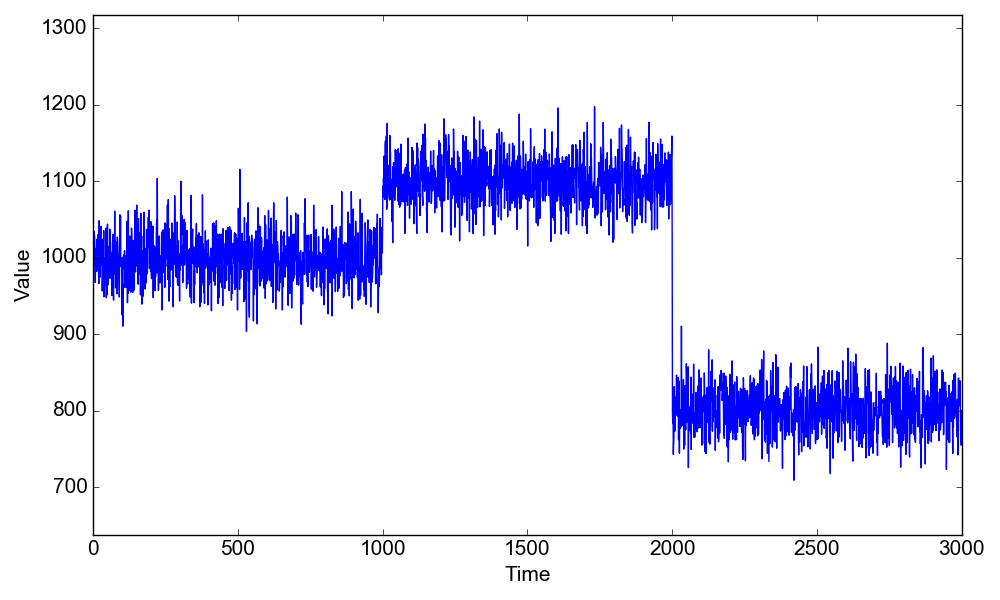
To find the posterior estimates for $\tau_1$, $\tau_2$, $\mu_1$, $\mu_2$ and $\sigma$,

1
2
3
4
5
6
7
8
9

In [4]: d.find_changepoint()
Assigned NUTS to mu1_interval_
Assigned NUTS to mu2_interval_
Assigned NUTS to mu3_interval_
Assigned Metropolis to tau1
Assigned Metropolis to tau2
Assigned NUTS to sigma_interval_
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████| 2000/2000 [00:46<00:00, 42.99it/s]
In [5]: d.plot_results()

The resulting trace plot is given below. As before, the posterior estimates are close to the true parameters.

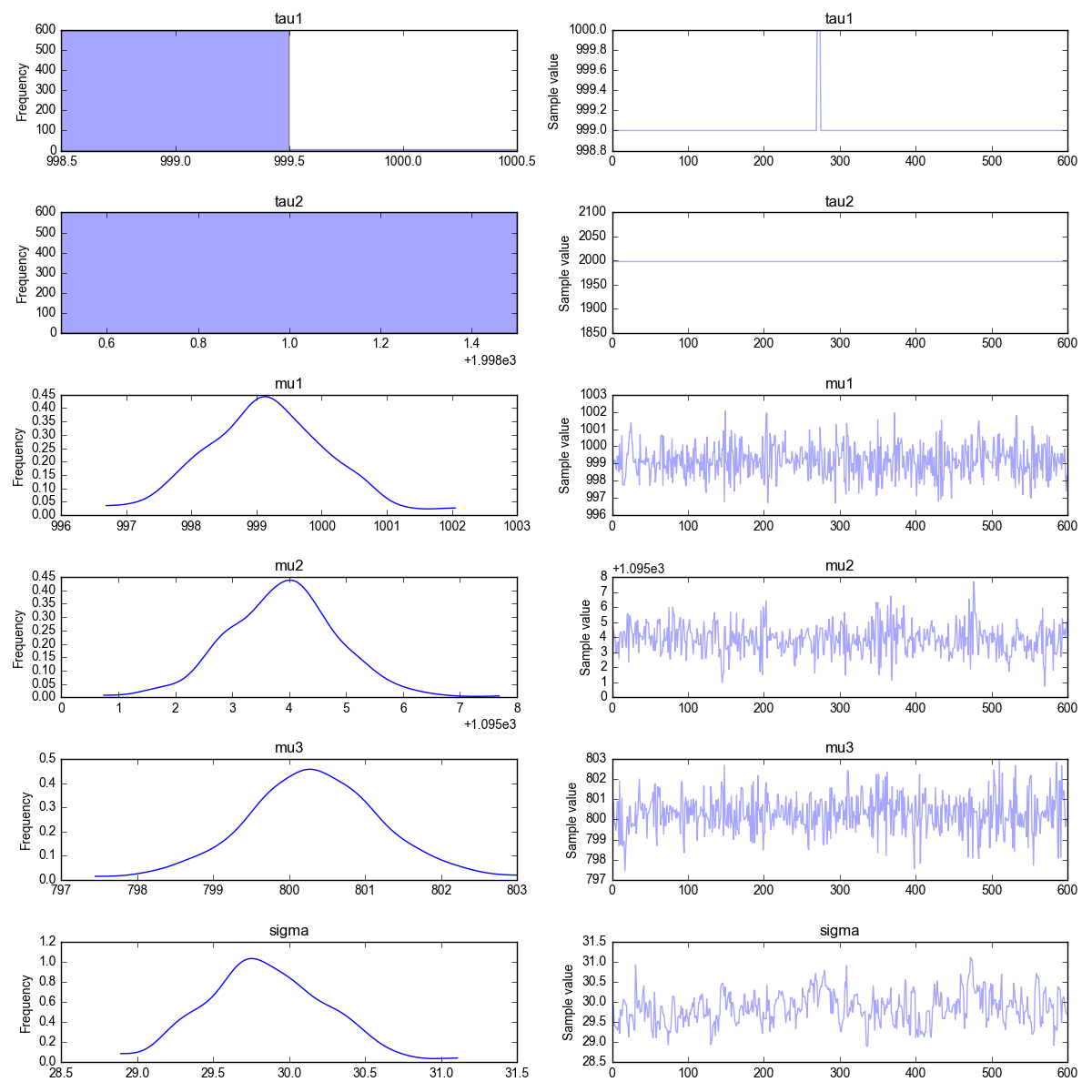
2.5 Three changepoints in the mean

This is our final problem. Here we are going to have not one, not two but three change points! The change point positions are $\tau_1=1000$, $\tau_2=2000$ and $\tau_3=2500$. The mean value changes from $\mu_1=1000$ to $\mu_2=1100$, then to $\mu_3=800$ and finally to $\mu_1=1020$. The standard deviation is kept constant at the value $\sigma=30$.

Again, we load and plot the data first:

1
2
3

In [1]: run changepoint_bayesian.py
In [2]: d = cpt_bayesian("3-cpt-mean")
In [3]: d.plot_data()

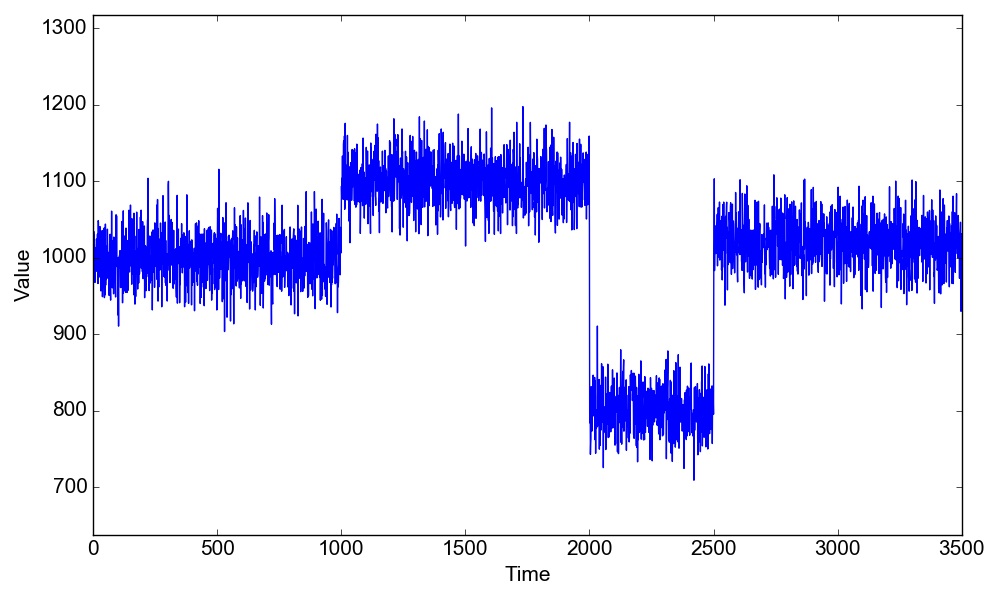
We have to estimate 8 parameters in this problem! They are $\tau_1$, $\tau_2$, $\tau_3$, $\mu_1$, $\mu_2$, $\mu_3$, $\mu_4$ and $\sigma$,

1
2
3
4
5
6
7
8
9
10
11

In [4]: d.find_changepoint()
Assigned NUTS to mu1_interval_
Assigned NUTS to mu2_interval_
Assigned NUTS to mu3_interval_
Assigned NUTS to mu4_interval_
Assigned Metropolis to tau1
Assigned Metropolis to tau2
Assigned Metropolis to tau3
Assigned NUTS to sigma_interval_
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████| 2000/2000 [02:18<00:00, 14.43it/s]
In [5]: d.plot_results()

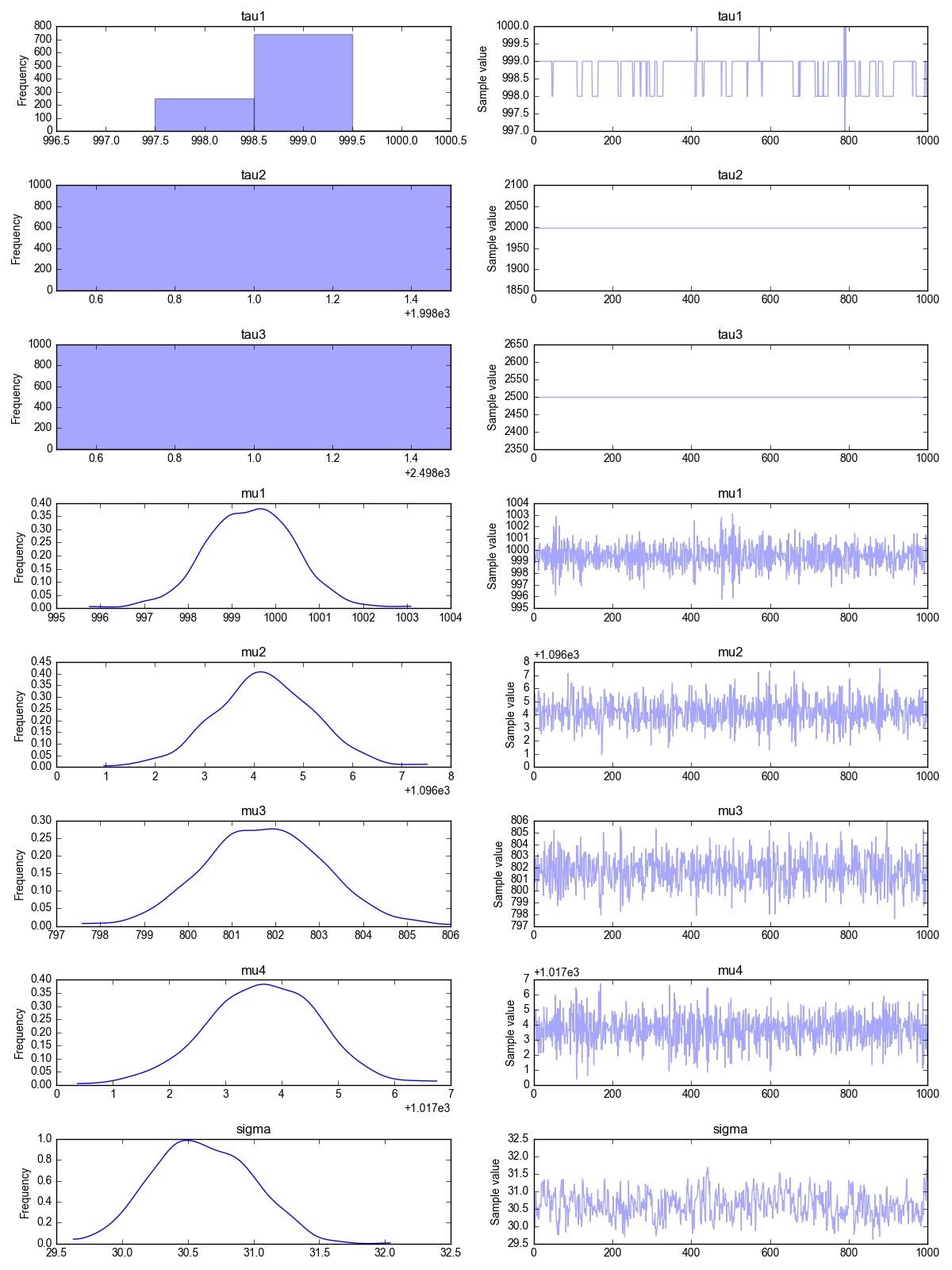
Once again, the trace plot shows that the MCMC algorithm has eventually converged. The Bayesian estimate for the model parameters are, once again, close to the true value. Good job $\small{\texttt{pymc3}}$!

References.

1. Numerical Bayesian Methods Applied to Signal Processing, by J. J. K. O Ruanaidh and W. J. Fitzgerald, Springer (1996)
2. For a tutorial on $\small{\texttt{pymc3}}$ that discusses the mine disaster example (a single change point problem), see this talk by John Salvatier
3. For more examples and more tutorials on $\small{\texttt{pymc3}}$, see the pymc3 website
4. For understanding Theano, other than the online documentation I found useful this video tutorial from NVIDIA (which is focused on deep learning as you might imagine)